| ■ 自動制御の話【4】 PID制御のシミュレーション
|
|
2.2 制御対象のステップ応答
前項にて制御対象を数式で表現することができましたが,PID制御を行なう場合は,最適
なパラメータを設定しなければ,よい応答(出力)は期待できないどころか,制御対象や制
御系全体の破損など危険な場合もあります.
ここでは,最もポピュラーなパラメータ設定法であるジーグラー・ニコルスのステップ応答
法でパラメータを設定します.表1-1及び図1-5参照
| P制御 |
Kp=τ/k・L |
Ti=∞ |
Td=0 |
| PI制御 |
Kp=0.9τ/K・L |
Ti=3.3L |
Td=0 |
| PID制御 |
Kp=1.2τ/K・L |
Ti=2L |
Td=0.5L |
表1-1 ジーグラ,ニコルスによる最適調整の係数(振幅減衰率1/4)
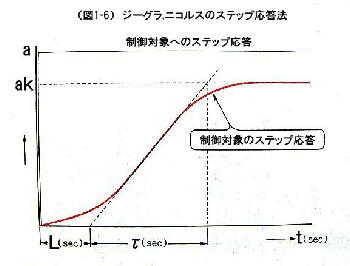 |
制御対象の応答,図1-6
より,
k=ak/a=0.333
L=20(sec)+T
=30(sec)
τ=165(sec)
が求まります.
ただし
T:サンプリング周期
=10(sec)
|
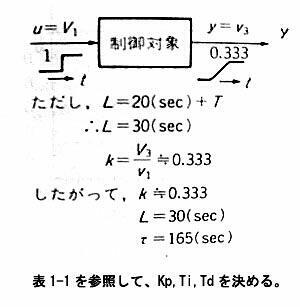 |
このように,ジーグラー・
ニコルスのPIDパラメータ
設定法(ステップ応答法)
では,制御対象(例では2
次遅れ要素)を「むだ時間
+1次遅れ」で近似しま
す.
また,ディジタル制御の場
合では,演算処理にかか
る時間またはサンプリン
グ周期を制御対象の「む
だ時間」の一部とみなし処
理します.
|
3. PID制御
3.1 P制御とシミュレーション
まずPID制御との比較のためにP制御のシミュレーションをしてみます.
P制御は比例制御ともよび,入力(偏差)と出力(操作量)との間に比例関係がなり立つ制
御で入出力関係は次式で示されます.
u(t)=kp・e(t) (5)
ただし、【u(t):操作量,kp:比例ゲイン,e(t):偏差】
k,L,τが前章にて求まりましたので,ジーグラー・ニコルスの設定条件(表1-1参照)よ
りパラメータを設定します.したがって、Kp=τ/(k*L)=16.52 となりますが、かなり
の偏差が残ってしまいます。P制御のシミュレーション結果を図1-7に示します.
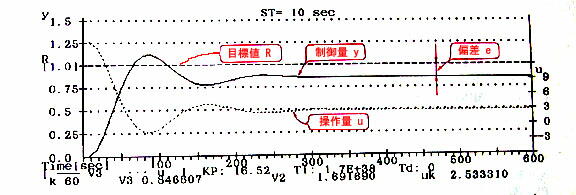
図1-7 P制御のシュミレーション結果
3.2 PI制御とシミュレーション
同様にPI制御のシミュレーションをしてみます.
PI制御は比例積分制御ともよび,入出力関係は(6)式で示され,目標値の変更や定常的
な外乱があっても偏差(誤差)を生じさせないという特長があります.

ジーグラ・ニコルスの設定条件(表1参照)よりPI制御のパラメータ,
kp=0.9τ/(k*L)=14.86 , Ti=3.3*L=99
が求まります.PI制御のシミュレーション結果を図1-8に示します.
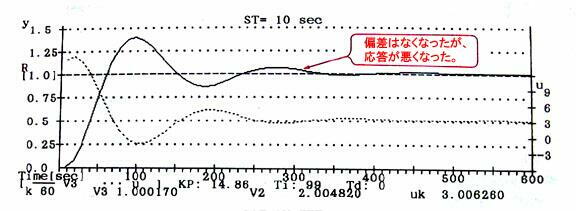
図1-8 P制御のシュミレーション結果
3.3 PID制御とシミュレーション
PID制御は比例積分微分制御ともよび積分動作における偏差をなくす性質と微分動作の
振動を制動させる性質を取り入れてP動作と組み合わせたもので,偏差がなく即応性の
よい応答を実現できます.
位置型PID制御器の入出力関係式は次式であらわせます.

ジーグラー・ニコルスの設定条件(表1参照)より
kp=1.2τ/(k*L)=19.82 , Ti=2*L=60 , Td=0.5*L=15
が求まります.PID制御のシミュレーション結果を図1-9に示します.
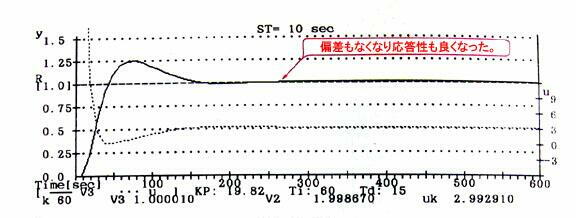
図1-9 PID制御のシミュレーション結果
4. あとがき
シミュレーションの結果を見ても,P制御,PI制御,PID制御の応答が異なることが解ると
おもいます.特にP制御はかなりの偏差(誤差)が残りますし,PI制御ですと定常状態にな
る時間が長くかかります.またリミッタのかけかたによっても応答が変わります.
DDCを行なう場合は,D/A変換器からの出力は±1v〜±10v程度しか得ることができ
ないので,その範囲でリミッタをかけなければD/A変換器がオーバーフローしてしまい出
力が不正確になってしまいます.
今回は,ディジタルPID制御(位置型)のパラメータの設定方法とシミュレーションを中心
に説明しましたが,実際の制御対象は,非線形の部分があるためシミュレーション通りに
いかないのが現実です.
この場合,kp,Ti,Tdの各パラメータを微調整することにより,ほぼ目的にかなった応答
を得ることができます.
文責
北海道大学 情報科学研究科
技術専門職員 石川 栄一
自動制御に関するご質問は次のメールアドレス宛に送信して下さい。

|
|
|